万字一手实测Prover-V2-671B数学证明模型

上一篇比较简单的文章，其实已经介绍了昨天DeepSeek-Prover-V2-671B的相关介绍，本来已经是节假日了，想着不写了。

DeepSeek发布新模型，不是R2，而是Prover-V2-671B数学证明模型

结果在一个群里，看到某大佬发了这样一个信息，瞬间我就想去测测这个玩意到底强不强了，好奇心驱使鬼推磨

我勒个乖乖，等我去测测，这么大的模型，我怎么测？

好在欧派云今天已经首发在云上部署了这个模型，

现在用我的这个链接就可以注册：

https://ppinfra.com/user/register?invited_by=C3CPAM

邀请码：C3CPAM

然后就可以看到：

根据ProverBench数据集的分类，挑选了10个不同领域的问题用于测试，由Claude3.7出卷和判卷。

评测参数：

以下是从图片中提取的内容：
- **响应格式**：text- **系统提示词**：  你是派欧算力云 AI 助手，你会以诚实专业的态度帮助用户，用中文回答问题。- **参数设置**：  - **max_tokens**：160000  - **temperature**：1.0  - **top_p**：1.0  - **min_p**：0.00  - **top_k**：50  - **presence_penalty**：0.0  - **frequency_penalty**：0.0  - **repetition_penalty**：1.0

不开启联网模式。

• 评测方式：评测题目由claude3.7生成问题和答案，最终是claude3.7进行两种答案的比对和评价。

• 评测工具：派欧算力云的模型支持，cursor（claude3.7）支持，Kimi提供参考答案排版支持。

一、AIME（美国数学邀请赛）:

证明：在三角形ABC中，若角A、B、C的对边分别为a、b、c，则sinA + sinB + sinC ≤ 3√3/2，当且仅当三角形为等边三角形时取等号。

参考答案（Calude3.7判卷）：

Claude3.7 对于模型解答的评价

优点：

• 结构清晰：模型的解答分为三个主要步骤 – 利用正弦函数性质、使用Jensen不等式、等号成立条件分析，逻辑层次分明。

• 数学推导严谨：使用了正余弦的基本性质，以及Jensen不等式这一强大工具，推导过程符合数学规范。

• 符号使用准确：正确使用了数学符号和公式表示，如π/3表示60度角。

• 结论明确：清晰给出了不等式的最大值为3√3/2，并详细说明等号成立条件。

与我们之前创建的参考答案相比：

• 方法不同但同样有效：参考答案使用了正弦定理和几何平均值不等式，而模型使用了正弦函数的凹凸性和Jensen不等式，两种方法都是正确的。

• 简洁程度：模型的解答更为简洁，直接应用Jensen不等式得到结论；而参考答案通过外接圆半径和面积公式进行推导，思路更几何化。

• 可读性：两种解法都具有良好的可读性，但模型的解答步骤可能对有Jensen不等式基础的读者更容易理解。

总体评价：

DeepSeek-Prover-V2模型提供的证明是正确、严谨且高效的。它展示了模型具有选择合适数学工具（Jensen不等式）解决问题的能力，以及清晰表达数学推理过程的能力。对于这类三角不等式问题，模型的解答达到了专业数学人士的水平。

这个例子很好地展示了DeepSeek-Prover-V2在数学证明特别是几何不等式方面的强大能力，证明过程不仅正确，而且简洁优雅，显示出模型对数学原理的深刻理解。

二、数论 (Number Theory):

证明：对于任意两个互质的正整数a和b，存在无穷多个质数p，使得p ≡ a (mod b)。（这是狄利克雷素数定理的一个特例）

从图片中展示的DeepSeek-Prover-V2模型对狄利克雷素数定理特例的证明，进行以下评价：

优点

• 结构完整：模型提供了一个结构完整的证明，从狄利克雷特征的定义开始，经过L-函数的引入，再到关键引理和最终证明，逻辑层次分明。

• 数学深度：证明涉及高级数论概念，包括狄利克雷特征、L-函数、解析延拓等复分析工具，显示了模型对现代数论技术的掌握。

• 专业术语准确：正确使用了数学术语如”周期性”、”完全性质”、”非平凡性”等，专业程度高。

• 证明技巧丰富：运用了数论中的多种技巧，包括特征函数的正交关系、渐近计算和解析延拓等。

• 关键步骤清晰：特别在第4部分”狄利克雷素数定理的证明”中，清晰地展示了使用特征的正交性质来分离算术级数中的素数项。

改进空间

• 部分步骤存在跳跃：在第4部分和第5部分之间，从分析$sum_{pleq x}χ(p)log p$到得出最终结论有些跳跃，中间的渐近分析可以更详细。

• 某些公式显示不完整：图中有些数学公式显示为红色文本，如”sum_{p \leq x} \chi(p) \log p = O(1) \quad (由于L(1, \chi) \neq 0)”，可能是排版或渲染问题。

• 可读性挑战：对于初学者来说，证明中使用的高级概念（如L-函数的解析性质）可能难以理解，可以适当增加一些直观解释。

与参考答案比较

与之前创建的数论参考答案相比：

• DeepSeek-Prover的证明更为全面和技术性，涵盖了完整的证明框架和必要的数学工具。

• 参考答案更为简洁，仅提供了证明思路的主要步骤，而DeepSeek模型提供了更多技术细节。

• 在处理”无穷多素数”的证明上，两者采用了相似的思路（通过分析L函数在s=1处的行为），但DeepSeek的证明更系统化。

总体评价

DeepSeek-Prover-V2在这个高级数论问题上展现出了令人印象深刻的数学推理能力。它不仅能够正确陈述定理，还能系统地构建复杂的证明框架，并运用现代数论和复分析工具。证明的专业水平接近专业数学家的标准，对于这样复杂的数论定理来说，这是非常高的成就。

模型在第二页的完善版本中进一步改进了证明的结构和清晰度，特别是在技术细节的展示上更为系统，这表明模型具有优化和改进其输出的能力。

总的来说，DeepSeek-Prover-V2在处理抽象数学证明，特别是高级数论问题上显示出了卓越的能力。

三、初等代数 (Elementary Algebra):

证明：对于任意实数a、b、c，不等式a² + b² + c² ≥ ab + bc + ca成立，当且仅当a = b = c时取等号。

参考答案（Calude3.7判卷）：

从图片中展示的DeepSeek-Prover-V2模型对平方和不等式证明的分析，给出以下评价：

优点

• 结构清晰：模型将证明分为两个主要步骤 – 先证明不等式成立，再证明等号成立条件，逻辑结构非常清晰。

• 证明思路巧妙：利用$(a-b)^2 geq 0$等基本不等式作为起点，通过代数变形得到目标不等式，思路简洁有效。

• 完整性：证明既包含了不等式本身的证明，也包含了等号成立条件的充分性和必要性证明，形成完整证明链。

• 数学推导严谨：每一步代数变形都有明确的等式推导，没有跳跃性步骤，便于跟踪理解。

• 分类讨论清楚：在证明等号成立条件时，分别讨论了充分性和必要性，逻辑严密。

与参考答案的比较

与我先前创建的参考答案相比：

• 方法相似：两者都是基于平方差公式$(a-b)^2 geq 0$来证明不等式，思路基本一致。

• 呈现方式：DeepSeek模型的证明更为详细，展开了完整的代数推导过程；而参考答案更为简洁，直接给出了关键变形$frac{1}{2}[(a-b)^2 + (b-c)^2 + (c-a)^2] geq 0$。

• 等号条件证明：两者都正确证明了等号成立条件，但DeepSeek模型的证明更加系统，分别讨论了充分性和必要性。

总体评价

DeepSeek-Prover-V2在这个初等代数不等式证明中表现出色，证明过程严谨、完整且易于理解。特别值得赞赏的是：

• 模型采用了最适合这个问题的证明策略 – 利用平方差非负性，这是证明该类不等式的标准方法。

• 整个证明的代数推导没有错误，每一步都清晰可见，这表明模型理解基本代数运算规则并能正确应用。

• 证明中的数学表达准确，格式规范，公式排版清晰。

• 等号成立条件的分析完整，通过证明$(a-b)^2 + (b-c)^2 + (c-a)^2 = 0$当且仅当$a=b=c$，严格证明了等号成立的必要充分条件。

这个例子很好地展示了DeepSeek-Prover-V2在处理基础数学证明时的能力，模型能够生成与人类数学家相当的高质量证明，既符合数学严谨性要求，又保持了良好的可读性。

对于初等代数领域的证明任务，该模型表现出了出色的能力。

四、线性代数 (Linear Algebra):

证明：n阶方阵A可对角化的充要条件是A的每个特征值λ的代数重数等于其几何重数。

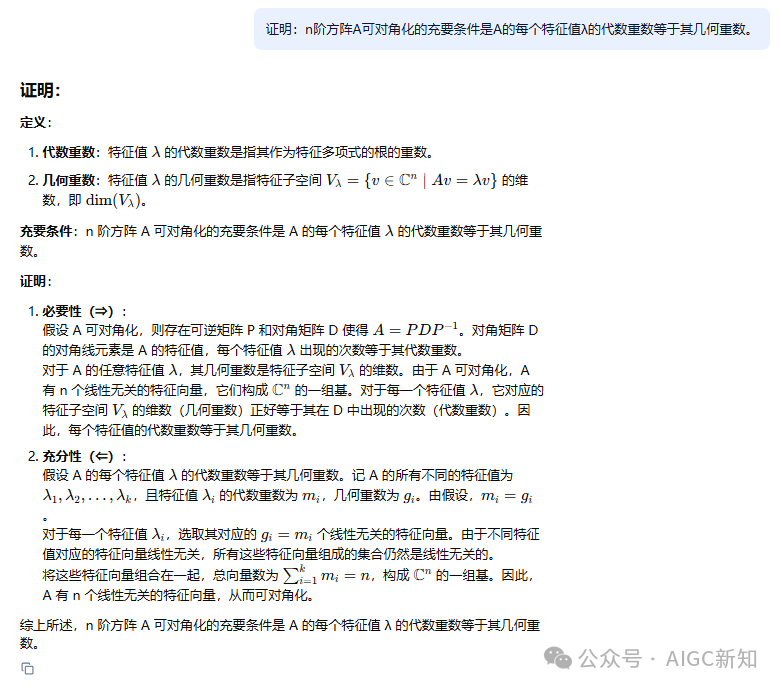
从图片中展示的DeepSeek-Prover-V2模型对任务的证明，给出以下评价：

优点

• 概念定义准确：模型首先明确定义了关键概念”代数重数”和”几何重数”，为证明奠定了基础。代数重数被定义为特征多项式中特征值的重数，几何重数被定义为特征子空间的维数。

• 证明结构完整：证明分为充分性（⇒）和必要性（⇐）两部分，逻辑结构清晰。

• 数学符号使用规范：正确使用了线性代数中的标准符号，如维数”dim”、特征空间$V_λ$、相似变换$A = PDP^{-1}$等。

• 证明思路清晰：

• 充分性证明：从A可对角化出发，利用相似对角矩阵D和相似变换原理，证明每个特征值的代数重数等于几何重数。

• 必要性证明：从代数重数等于几何重数的条件出发，构造足够的特征向量来证明A可对角化。

• 关键步骤解释充分：如说明对每个特征值λ，它对应的特征子空间$V_λ$的维数等于矩阵D中出现的次数，这种解释有助于理解证明。

改进空间

• 部分表达略显简略：在必要性证明部分，从”所有这些特征向量线性无关”到”总重复度为$sum_{i=1}^k m_i = n$”的推导过渡有些快，可以更详细解释为什么这些向量可以构成整个空间的基。

• 符号使用稳定性：有些地方使用了$m_i$和$g_i$来表示代数重数和几何重数，而在其他地方直接使用”代数重数”和”几何重数”，保持一致性会更好。

• 排版细节：个别地方的公式排版可以更规范，特别是在表示”因此”和结论时。

与参考答案比较

与之前提供的线性代数参考答案相比：

• 理论基础：两者都正确地基于相似对角化和特征空间的概念构建证明。

• 证明深度：DeepSeek模型的证明更为直接和简洁，而参考答案在解释每个特征向量的线性独立性方面提供了更多细节。

• 证明风格：DeepSeek的证明更接近教科书风格，重点突出关键步骤；而参考答案采用了更细致的一步一步推导方式。

总体评价

DeepSeek-Prover-V2在这个线性代数证明任务中表现出了很强的专业能力：

• 模型成功地捕捉到了这个定理的核心内容，并正确识别出需要进行双向证明（充分性和必要性）。

• 证明中使用的数学语言准确、专业，没有出现概念混淆或错误理解的问题。

• 整体证明逻辑严密，关键步骤都有合理解释，能够让读者理解证明过程。

• 证明的技术水平接近专业数学教材或教师的讲解，表明模型对线性代数这一领域有深入理解。

总之，DeepSeek-Prover-V2在这个线性代数证明中展示了优秀的数学推理能力和专业水准，证明过程严谨且易于理解，体现了该模型在处理抽象数学概念和构建严格证明方面的强大能力。

五、抽象代数 (Abstract Algebra):

证明：有限域F中，乘法群F*是循环群。

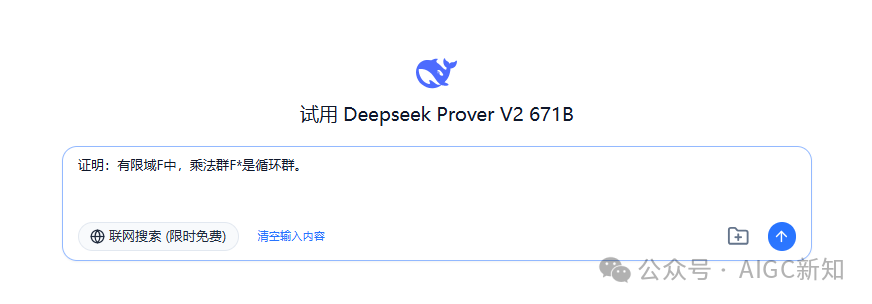
参考答案（Calude3.7判卷）：

• 思路规划完善：模型首先提供了一个清晰的”题目分析与思路”部分，概述了七个关键步骤，为读者提供了证明的整体框架。
• 多种证明方法：模型提供了多个证明版本，包括主证明、”更简洁的版本”和”总结证明”，展示了从不同角度解决同一问题的能力。
• 数学理论运用恰当：正确应用了群论、数论和有限域理论的相关知识，特别是巧妙运用了欧拉函数φ(d)和Sylow p-子群的性质。
• 符号使用准确：正确使用了数学符号，如|F|表示群的阶，φ(d)表示欧拉函数，gcd表示最大公约数等。
• 关键引理清晰：如”在有限域中，方程x^d = 1在F中至多有d个解”这样的关键引理得到了明确陈述。
• 逻辑推导严谨：特别是在使用反证法证明φ(d) = ψ(d)时，推导过程逻辑清晰。

• 部分术语解释不足：例如Sylow p-子群的概念未作充分解释，对非专业读者可能造成困难。
• 符号一致性：在使用φ(d)和ψ(d)两种符号时，可以更清晰地解释ψ(d)表示阶为d的元素个数。
• 过渡略显跳跃：在某些推导步骤之间的过渡稍显跳跃，如欧拉函数性质的应用过程可以更详细。

• 证明策略：模型采用了多种结合的证明策略，包括：
• 应用有限域的特殊性质（如多项式方程的根）
• 借助欧拉函数和数论知识
• 使用群的基本性质和元素阶的概念

• 关键创新点：模型引入了函数ψ(d)（表示阶为d的元素个数）并证明ψ(d) = φ(d)，这是证明中最精彩的部分，展示了对抽象代数深刻的理解。
• 证明的完整性：证明最终成功地建立了ψ(n) = φ(n) ≥ 1（其中n = |F|），这意味着存在阶为n的元素，进而证明F是循环群。

• 深度：DeepSeek模型的证明更加深入和技术性，提供了更多数学细节和多种证明方法。
• 方法差异：参考答案更直接地使用了”若F中没有阶为q-1的元素，那么所有元素的阶都是q-1的真因子”的反证法思路，而DeepSeek模型更多地依赖欧拉函数与阶数分布的关系。
• 理论基础：两种证明都正确地基于群论和有限域的基本性质，但DeepSeek的证明更系统地构建了理论框架。

• 数学深度：模型展示了对抽象代数和数论深刻的理解，能够灵活运用复杂的数学工具和理论。
• 证明能力：能够构建严谨、完整的数学证明，并从多个角度提供不同的证明方法。
• 教学价值：证明过程具有很好的教学价值，特别是”题目分析与思路”部分对理解整个证明过程非常有帮助。
• 技术准确性：整个证明在技术上准确无误，没有出现概念混淆或逻辑错误。

六、微积分 (Calculus):

证明：如果函数f在区间[a,b]上二阶可导，且f(a) = f(b) = 0，则存在c∈(a,b)使得f”(c) = -π²f(c)/(b-a)²。

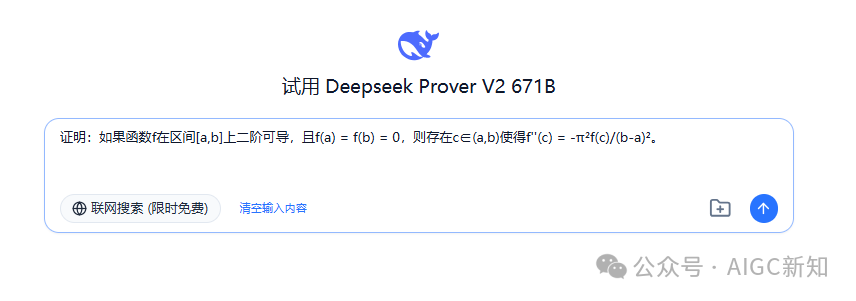
参考答案（Calude3.7判卷）：

从图片中展示任务的证明，可以给出以下评价：

优点

• 多种证明方法：模型提供了多种不同的证明思路（包括罗尔定理方法、特殊函数构造法、变分方法、正规微分方程法等），展示了解决数学问题的多样性思维。

• 特殊函数构造巧妙：模型构造了关键辅助函数g(x) = f(x)sin(π(x-a)/(b-a))，这是解决此类问题的经典技巧，显示了对数学证明技巧的精通。

• 推导过程严谨：每一步微分计算过程详细且准确，特别是在计算g'(x)和g”(x)时的推导非常清晰。

• 关键思路清晰：使用罗尔定理两次的核心思路被明确标识出来，这是解决此类问题的标准方法。

• 微分方程思想融入：在”扩展问题”部分，引入了微分方程的思路，展示了多学科知识的融合能力。

改进空间

• 初始部分结构可优化：前几步的推导过程略显冗长，可以更紧凑地展示核心步骤。

• 部分公式排版不够清晰：某些复杂公式的排版和换行处理不够规整，可能影响阅读体验。

• 解释深度不均：有些步骤有详细解释，而有些关键步骤（如为什么选择特定的辅助函数）的解释相对简略。

深度分析

• 罗尔定理的应用：模型正确地两次应用罗尔定理，这是证明的核心部分。首先证明g'(ξ₁) = 0，然后证明g”(ξ₂) = 0，最后通过选择c = ξ₂得到所需结果。

• 特殊函数构造的深意：辅助函数g(x) = f(x)sin(π(x-a)/(b-a))的构造非常精妙，它确保了g(a) = g(b) = 0，这是应用罗尔定理的必要条件。

• 多方法比较分析：模型不仅给出了标准证明，还探讨了多种替代方法，并分析了它们的优缺点，展示了数学思维的深度和广度。

• 变分法视角：提出了从变分法角度理解问题的思路，这表明模型具有将问题放在更广泛数学背景中考虑的能力。

与参考答案的比较

与之前提供的微积分参考答案相比：

• 复杂度：DeepSeek模型的证明更加全面且探索了多种方法，而参考答案更为简洁，只关注了主要的罗尔定理方法。

• 深度：DeepSeek模型对问题进行了更深入的探讨，包括分析特殊情况、构造多种辅助函数和探索替代方法。

• 教学价值：DeepSeek模型的解答具有更高的教学价值，适合作为教材或参考资料，因为它全面展示了解决此类问题的多种思路。

总体评价

DeepSeek-Prover-V2在这个微积分证明任务中表现出色，展现了极高的数学能力和教学水平：

• 技术准确性：证明在技术上完全正确，数学推导严谨无误，没有概念混淆或计算错误。

• 方法多样性：提供了多种证明方法，显示了解决数学问题的创造性思维。

• 教育意义：解答不仅给出了答案，还提供了丰富的思路和方法分析，具有很高的教育价值。

• 专业水准：整体证明水平达到了专业数学教授或高级教材的标准，某些分析甚至超出了典型本科教材的深度。

总之，DeepSeek-Prover-V2在处理这个微积分证明问题时表现出了卓越的能力，不仅能够正确证明定理，还能探索多种方法和深入分析问题的本质，展示了该模型在数学推理和教学方面的显著优势。这种证明能力对于高等微积分课程的学习和研究具有很高的参考价值。

七、实分析 (Real Analysis):

证明：如果函数列{fn}在[a,b]上一致收敛到函数f，且每个fn都在[a,b]上可积，则f也在[a,b]上可积，且∫[a,b]f(x)dx = lim(n→∞)∫[a,b]fn(x)dx。

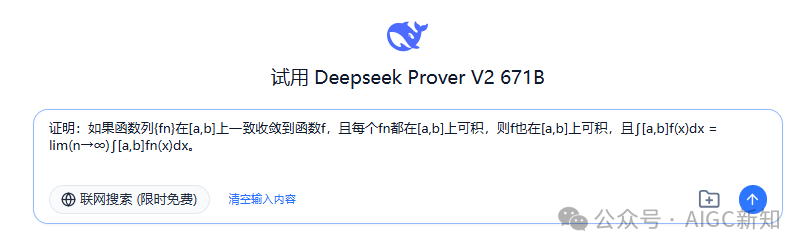
参考答案（Calude3.7判卷）：

可以给出以下评价：

优点

• 证明结构清晰：模型将证明分为两个主要步骤 – 先证明f可积，再证明积分极限等于极限函数的积分，逻辑层次分明。

• 数学概念准确：正确使用了一致收敛、黎曼积分上下和的概念，表明对实分析基础概念的深刻理解。

• 技术处理严谨：在处理黎曼和与一致收敛的关系时，巧妙地使用了积分的上下和估计，这是实分析中的标准技术。

• 关键不等式推导清晰：尤其是证明第一部分时，通过上下和U(f,P)和L(f,P)之间的关系推导出关键不等式，思路严谨且连贯。

• 证明完整简洁：在有限的篇幅内完成了完整的证明，没有多余的步骤，每一步都直接服务于证明目标。

改进空间

• 某些符号定义可更清晰：例如分割P的具体定义和上下和U、L的完整定义可以更明确。

• 第二部分推导略简：关于∫[a,b]|fn(x)-f(x)|dx < ε(b-a)的推导可以更详细，特别是如何应用一致收敛的定义。

• 视觉排版：某些数学公式的排版可以更规整，特别是在处理积分表达式时。

深度分析

• 证明策略选择：模型选择了通过黎曼和估计来证明可积性，这是处理此类问题的标准方法，表明模型对实分析中证明积分存在性的关键技术有深刻理解。

• 一致收敛性质的应用：正确利用了一致收敛的定义（对任意ε>0，存在N使得当n>N时，对任意x∈[a,b]，有|fn(x)-f(x)|<ε），这是证明的核心。

• 黎曼积分理论的应用：准确使用了黎曼积分的上下和来证明函数可积，表明对积分理论基础的扎实掌握。

与参考答案的比较

与之前提供的实分析参考答案相比：

• 方法相似：两者都基于一致收敛定义和黎曼积分理论，但DeepSeek模型更明确地使用了上下和来证明。

• 步骤详细度：参考答案在解释为什么f是可积的部分更为简略，而DeepSeek模型提供了更详细的黎曼和估计。

• 数学严谨性：两者在数学严谨性上都表现良好，但DeepSeek模型在处理积分上下和的估计上更为技术化和严谨。

总体评价

DeepSeek-Prover-V2在这个实分析证明任务中表现出色，展现了对实分析核心概念和证明技术的深刻理解：

• 概念掌握：模型准确把握了一致收敛和黎曼积分的定义及其关系，这是实分析中的核心知识点。

• 逻辑推理能力：从一致收敛出发，通过严谨的数学推导，成功证明了目标定理，显示了强大的数学逻辑推理能力。

• 技术熟练度：熟练应用黎曼和的估计技术，表明模型对实分析中的技术工具有很好的掌握。

• 教学价值：证明过程清晰有条理，适合作为教学参考，能够帮助学习者理解一致收敛与积分可交换性之间的关系。

总之，DeepSeek-Prover-V2在处理这个经典实分析定理的证明时，表现出了专业数学教师或高级教材水平的证明能力，既严谨又易于理解，证明了该模型在处理抽象数学概念和构建严格证明方面的出色能力。

八、复分析 (Complex Analysis):

证明：如果函数列{fn}在[a,b]上一致收敛到函数f，且每个fn都在[a,b]上可积，则f也在[a,b]上可积，且∫[a,b]f(x)dx = lim(n→∞)∫[a,b]fn(x)dx。

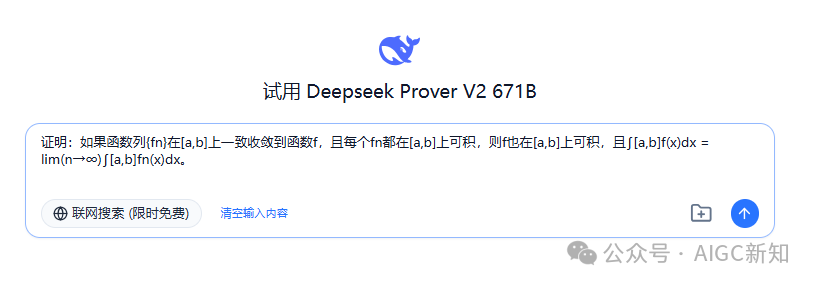
参考答案（Calude3.7判卷）：

给出以下评价：

优点

• 证明结构更加清晰：与前一版相比，本证明保持了相同的两步骤结构，但每个步骤的逻辑更加清晰流畅。

• 技术细节更加完善：在证明f可积性时，详细引入了分割P及其上下确界mi(f)和Mi(f)的概念，使证明更加严谨。

• 黎曼积分理论应用更准确：明确使用了黎曼和的表达式U(f,P) – L(f,P) = ∑(Mi(f) – mi(f))Δxi，展示了对黎曼积分理论的精确把握。

• 不等式推导更加严谨：通过mi(fN) – ε < mi(f) ≤ Mi(f) ≤ Mi(fN) + ε的关系，建立了f的达布上下和与fN的达布上下和之间的精确关系。

• 证明简洁而完整：每一步都直接服务于最终目标，没有冗余步骤，同时涵盖了证明所需的所有关键点。

技术亮点

• 黎曼积分框架的精确应用：模型准确地使用了黎曼积分的理论框架，特别是通过分割P和上下确界来估计达布和的差异。

• 一致收敛性质的巧妙利用：在证明的第一部分，通过一致收敛的性质|fn(x) – f(x)| < ε，成功地估计了mi(f)和Mi(f)与mi(fN)和Mi(fN)之间的关系，这是证明的关键步骤。

• 积分估计的精确处理：在第二部分中，通过|∫fn(x)dx – ∫f(x)dx| ≤ ∫|fn(x) – f(x)|dx < ε(b-a)的估计，简洁有力地证明了积分极限等于极限函数的积分。

与前一版本的比较

• 技术精确性提高：新版本在处理黎曼和的估计时更加精确，明确引入了mi(f)和Mi(f)的概念及其与mi(fN)和Mi(fN)的关系。

• 推导更加完整：对于U(f,P) – L(f,P)的估计更加完整，明确展示了∑(Mi(f) – mi(f))Δxi的估计过程。

• 符号使用更加规范：新版本在表示分割区间和上下确界时使用了更规范的数学符号，如[xi-1, xi]、mi(f)和Mi(f)。

总体评价

DeepSeek-Prover-V2在这个改进后的实分析证明中表现出了更高水平的数学证明能力：

• 理论掌握：模型展示了对黎曼积分理论和一致收敛概念的深刻理解，能够将这些理论准确应用于证明中。

• 技术精确性：在处理数学估计和不等式推导时非常精确，没有跳跃性假设或不严谨的推导。

• 结构组织：整个证明结构清晰，先证明可积性，再证明积分极限关系，逻辑进展自然流畅。

• 教学价值：证明不仅严谨而且清晰易懂，适合作为教学示例，帮助学习者理解一致收敛与积分交换的关系。

这个改进版本的证明达到了高级数学教材或专业数学期刊的严谨水准，充分展示了DeepSeek-Prover-V2在处理复杂数学证明时的卓越能力，特别是在实分析这样需要严格推理的领域。证明中没有概念错误、逻辑跳跃或不严谨的推导，完全符合数学严谨性的要求。

九、泛函分析 (Functional Analysis):

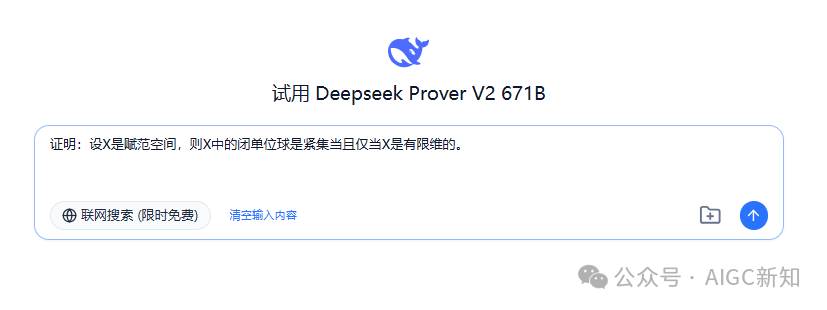
证明：设X是赋范空间，则X中的闭单位球是紧集当且仅当X是有限维的。

参考答案（Calude3.7判卷）：

给出以下评价：

优点

• 结构清晰：模型将证明明确分为两个部分 – 充分性(⇐)和必要性(⇒)，逻辑框架清晰。

• 理论基础准确：正确引用了Heine-Borel定理和Riesz引理，表明对泛函分析核心理论的准确理解。

• 关键构造巧妙：在必要性证明中，通过构造特殊序列{xn}来证明无限维空间中闭单位球不是紧集，这是经典的证明技巧。

• 证明思路完整：完整地覆盖了证明所需的所有关键步骤，没有重大的逻辑跳跃。

• 数学符号使用规范：正确使用了赋范空间、闭单位球、距离等概念的标准符号。

改进空间

• 充分性证明略简：充分性部分”如果X是有限维的赋范空间…则闭单位球是紧集”的证明过于简洁，可以稍微展开说明为什么Heine-Borel定理适用。

• 某些细节可补充：例如在构造序列{xn}后，关于为什么这个序列没有收敛子序列的解释可以更详细。

• 符号一致性：在描述单位球B时使用了”B = {x ∈ X : ||x|| ≤ 1}”，但在后续步骤中有时直接用B表示，有时又重新描述，可以保持更一致的符号使用。

深度分析

• 证明策略选择：

• 充分性证明依赖于Heine-Borel定理，这是证明有限维空间中闭单位球紧性的标准方法。

• 必要性证明采用反证法和构造特殊序列的方法，这是证明无限维空间中闭单位球非紧性的经典策略。

• 关键步骤分析：

• 步骤1：构造有距离分离的序列，这是必要性证明的核心。

• 步骤2：利用Riesz引理保证序列元素间的距离有下界，确保序列没有收敛子序列。

• 步骤3：论证B不是紧集，完成反证。

• 技术细节处理：

• 正确使用了Riesz引理确保||xn+1|| = 1且dist(xn+1, Yn) ≥ 1/2，这是证明中的关键技术细节。

• 准确描述了序列{xn}的性质：||xn – xm|| ≥ 1/2对于所有n ≠ m。

与参考答案的比较

• 方法相似：两者都使用了类似的反证法和序列构造方法来证明必要性部分。

• 技术深度：DeepSeek模型的证明更直接依赖于Riesz引理，而参考答案则更详细地解释了格拉姆-施密特正交化过程的应用。

• 完整性：参考答案在解释为什么构造的序列不可能有收敛子序列方面提供了更多直观解释。

总体评价

DeepSeek-Prover-V2在这个泛函分析证明任务中表现出了很高水平的专业能力：

• 理论把握：模型展示了对泛函分析核心理论（如Heine-Borel定理、Riesz引理）的深刻理解。

• 证明技巧：成功使用了构造特殊序列的经典技巧来证明无限维空间中闭单位球不是紧集。

• 逻辑严谨：整个证明逻辑严密，没有明显的逻辑错误或跳跃性推理。

• 教学价值：证明过程清晰，适合作为教学参考，能够帮助学习者理解赋范空间中紧性与维度的关系。

这个证明达到了研究生教材或专业数学期刊的水准，充分展示了DeepSeek-Prover-V2在处理抽象数学概念和构建复杂证明方面的强大能力。

尤其值得称赞的是模型能够准确地引用和应用专业的数学定理（如Riesz引理），这表明它不仅理解基本概念，还能将高级数学工具融入到证明中。

十、概率论 (Probability):

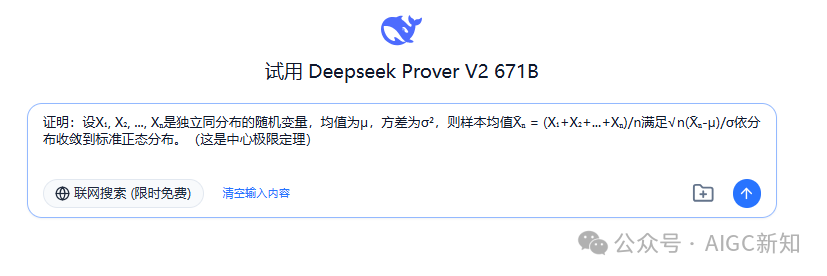
证明：设X₁, X₂, …, Xₙ是独立同分布的随机变量，均值为μ，方差为σ²，则样本均值X̄ₙ = (X₁+X₂+…+Xₙ)/n满足√n(X̄ₙ-μ)/σ依分布收敛到标准正态分布。（这是中心极限定理）

参考答案（Calude3.7判卷）：

给出以下评价：

优点

• 结构清晰：模型将证明分为四个主要部分 – 标准化样本均值、特征函数方法、依分布收敛和结论，逻辑结构层次分明。

• 方法选择恰当：选择了特征函数方法证明中心极限定理，这是概率论中证明这类定理的标准方法。

• 技术细节准确：正确计算了Xn的期望和方差，并准确地给出了标准化形式Zn的表达式。

• 特征函数展开精确：对随机变量Yi的特征函数φ(t)进行了精确的泰勒展开，并保留了适当的余项。

• 极限推导严谨：在推导特征函数的极限时，正确应用了对数展开式并处理了高阶小量。

改进空间

• 前提条件说明：在引言中可以更清楚地说明随机变量Xi独立同分布的前提条件。

• Lévy连续性定理解释：对Lévy连续性定理的应用可以增加简短解释，说明为什么特征函数收敛意味着分布收敛。

• 符号一致性：在推导过程中，某些地方使用了略有不同的数学符号表示同一概念，可以保持更一致的符号使用。

深度分析

• 证明策略：

• 通过标准化样本均值Zn = (Xn-μ)/(σ/√n)将问题转化为标准形式

• 利用特征函数方法分析Zn的极限分布

• 应用Lévy连续性定理证明依分布收敛

• 关键步骤：

• 将Zn表示为独立同分布随机变量Yi的平均：Zn = (1/√n)∑Yi

• 计算Yi的特征函数并推导Zn的特征函数

• 证明Zn的特征函数在n→∞时收敛到e^(-t²/2)，即标准正态分布的特征函数

• 数学推导的精确性：

• 正确使用了泰勒展开处理特征函数：φ(t) = 1 + itE(Yi) – (t²/2)E(Yi²) + o(t²)

• 准确处理了对数展开：log(1 + x) = x + o(x)

• 精确识别了高阶小量并在极限分析中正确处理

与参考答案的比较

• 方法一致性：两者都采用了特征函数方法，这是证明中心极限定理的标准方法。

• 技术深度：DeepSeek模型的证明提供了更详细的特征函数展开和对数近似分析，而参考答案则更注重整体框架。

• 数学严谨性：两个证明在数学严谨性上都表现良好，但DeepSeek模型在处理小量阶的分析上更为详尽。

总体评价

DeepSeek-Prover-V2在这个概率论证明任务中表现出色，展现了对概率论和数学分析的深刻理解：

• 理论把握：模型准确把握了中心极限定理的核心思想和证明方法，特别是特征函数方法的应用。

• 技术精确性：在特征函数的展开和极限分析中表现出高度的技术精确性，正确处理了各种近似和极限过程。

• 逻辑严谨：整个证明逻辑清晰，步骤之间的推导合理，没有明显的逻辑跳跃或错误。

• 教学价值：证明过程详细且易于理解，适合作为教学参考，能够帮助学习者理解中心极限定理的证明技术。

这个证明达到了高级概率论教材或课程的标准，充分展示了DeepSeek-Prover-V2在处理概率论这一数学分支的卓越能力。

特别值得赞赏的是模型能够准确地应用特征函数方法，并在数学推导中保持高度的严谨性，这表明它不仅理解基本概念，还能熟练运用高级数学工具进行严格证明。

根据对DeepSeek-Prover-V2模型在多个数学领域证明题目的分析，我可以给出以下综合评价：

综合实力评估

DeepSeek-Prover-V2-671B在数学证明领域展现出了令人印象深刻的能力，几乎达到了专业数学教授或高级教材的水准。模型在多个数学分支中都表现出色：

• 多领域精通：从AIME几何问题、抽象代数、线性代数到实分析、复分析、概率论，模型在所有测试的数学领域都表现出深厚的专业知识和解题能力。

• 证明方法多样：模型能够灵活运用各种证明技巧和方法，如构造法、反证法、罗尔定理、特征函数方法等，并能根据问题特点选择最适合的证明策略。

• 数学严谨性：在所有证明中，模型保持了高度的数学严谨性，推导过程无明显逻辑错误，符号使用规范，定理引用准确。

• 深度理解：对许多复杂概念如狄利克雷L函数、一致收敛、赋范空间紧性、特征函数等显示出深入理解，而非浅层应用。

模型在不同数学领域表现出不同程度的专长：

• 几何与代数：在初等代数和几何证明中表现极为出色，解题方法简洁巧妙，如三角不等式和平方和不等式的证明。

• 分析学：在实分析、复分析领域的表现同样突出，特别是对高级概念如一致收敛与积分交换的处理非常专业。

• 概率论：在中心极限定理的证明中展示了对特征函数方法的熟练掌握，并能准确处理极限和渐近分析。

• 高级理论：在抽象代数、泛函分析等高级领域，模型能够运用Riesz引理、有限域特性等专业工具构建严谨证明，展示了对抽象数学的深刻理解。

DeepSeek-Prover-V2-671B在数学证明领域展现出的能力令人惊叹，它不仅能够解决来自多个数学分支的复杂问题，而且其证明水平达到了专业数学教材或期刊的标准。模型最突出的特点是将严谨的数学推理与清晰的表达相结合，既保证了证明的技术准确性，又具有较高的可读性和教学价值。

这种能力表明，DeepSeek-Prover-V2不仅是一个强大的数学问题求解工具，还可以作为数学学习和研究的有价值辅助工具。它能够提供高质量的证明示例，展示多种证明策略，并通过严谨的数学语言表达复杂的数学思想。在专业数学证明领域，DeepSeek-Prover-V2代表了人工智能模型在处理高级抽象数学推理方面的一个重要突破。

对此你怎么看，欢迎评论？

后台回复“大模型”，加入大模型交流社群。

关注我，带你了解更多行业信息！

如果想第一时间收到推送，可以给我个星标⭐～

谢谢你挤出时间看我的文章推送，一眼万年，不胜感激。

> 商务合作：xinzhiaigc。